Introduction
Click on the tabs below for a (hopfully) accessible introduction to this area of research.
Special functions and elliptic functions
Special functions can be loosely defined as those mathematical functions with established names and notations due to their importance. This is often apparent from the formulae and properties they satisfy and their use in other branches of mathematics. A simple example would be the trigonometric functions.
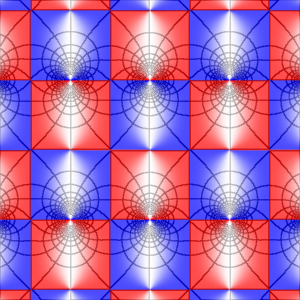
The high point of special function theory in the later 1800s was the theory of elliptic functions. These are essentially those functions of a complex variable that have two independent periods, (the values it takes repeat as you move in one of two directions). Hans Lundmark's Complex Analysis webpage gives a nice introduction with some excellent visualisations making the key properties clear. For example, the plot here is an elliptic function with the values taken (and hence patterns) repeating both horizontally and vertically.
The Weierstrass ℘-function is a particular type of elliptic function with a simple form and many useful properties. My work on Abelian functions could be summarised as the higher genus generalisation of Weierstrass elliptic function theory.
Abelian functions associated with algebraic curves
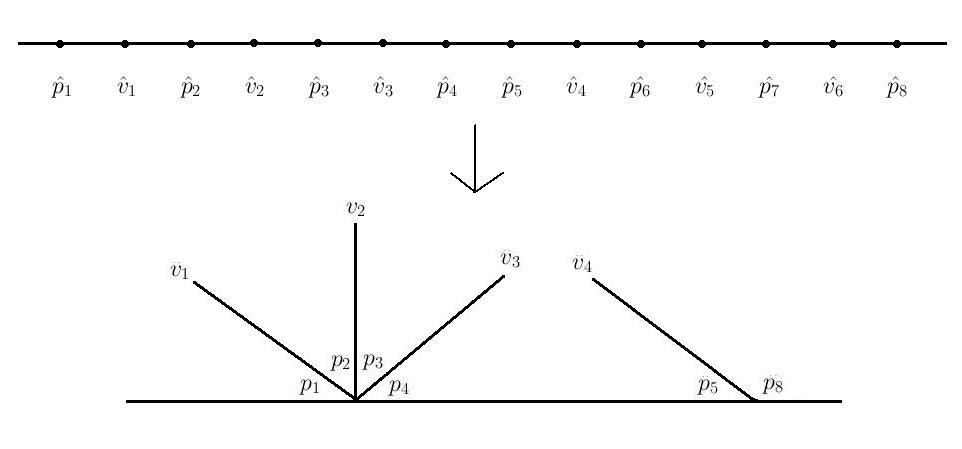
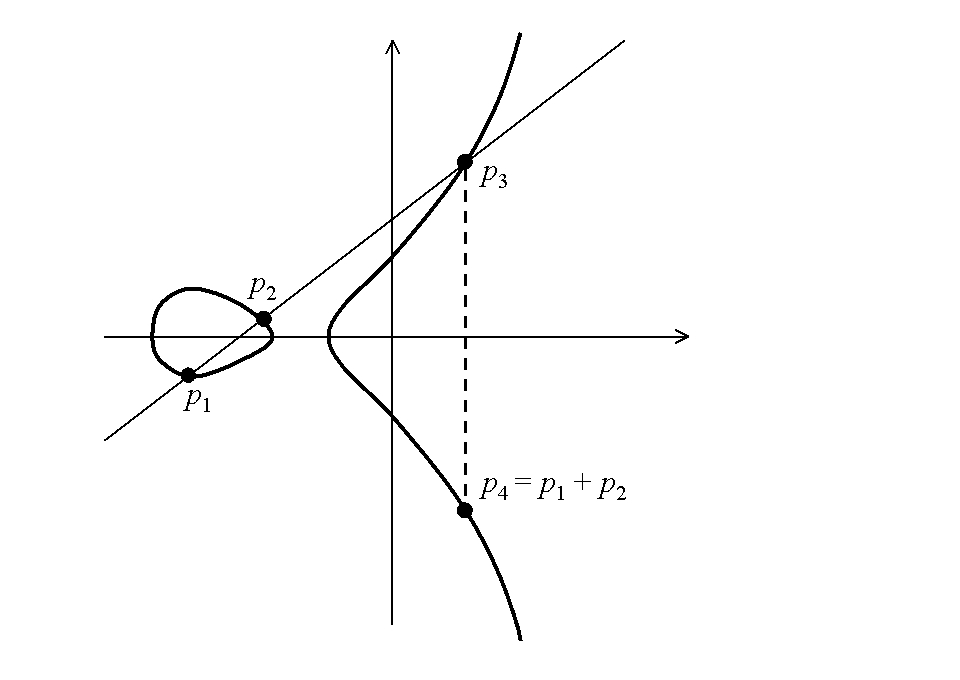
An Abelian function is a meromorphic function that has multiple periods. The functions can be defined using the periodicity properties of algebraic curves, leading to the curves as a classification system.
Kleinian ℘-functions are particular Abelian functions defined in analogy to the Weierstrass ℘-function, and satisfying similar properties. The main difference is that they are now functions of g variables where g is the genus of the algebraic curve used.
I have worked extensively with such functions investigating the addition formulae, differential equations, power series expansions and other properties that they satisfy. The theory lies within the fields of complex analysis and algebraic geometry. Their study has involved both new theory and intelligent use of symbolic computation. They have applications throughout mathematical physics and are perhaps best know as solutions to the KP-Heirarchy of integrable systems .

The KP-Heiratchy of equations can model water waves, offering the possibility to better understand tsunamis. The image is of The Great Wave off Kanagawa by Hokusai which has come to represent both tsunamis and the mathematica work in this area.
Application of Abelian functions
Applications of Abelian functions theory include use in soliton theory, describing the Kummer surface, modelling the motion of a double pendulum and describing geodesics in black hole spacetimes.

A soliton created in a lab. See here for one in real life.

Simulated view of a black hole.

An example of a Kummer Surface.
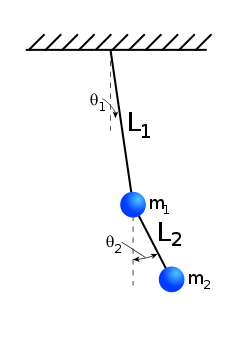
A diagram of a double pendulum.